Jak już pewnie wiesz najcięższym tematem dla wielu na egzaminie krótkofalarskim jest radiotechnika, a tym bardziej decybele. Dziś w prosty sposób o tym jak liczyć zadania z decybelami!
Logarytmy
Zanim zaczniemy odrobina przypomnienia z matematyki czym są logarytmy. Jest to operacja mówiąca o tym do jakiej potęgi należy podnieść liczbę w podstawie logarytmu (tę mniejszą), żeby otrzymać liczbę logarytmowaną. Po matematycznemu zapiszemy to tak: $$ \log_{a}b=x \Leftrightarrow a^x=b $$
Czym są decybele?
Decybel jest to jednostka służąca do porównywania ze sobą dwóch wartości. Używamy ich wtedy kiedy potrzebujemy porównać wartości zmieniające się liniowo w bardzo szerokim zakresie.
Załóżmy, że wykonaliśmy 7 pomiarów mocy jakiegoś urządzenia. Chcemy zobaczyć jak te wartości zmieniają się na przestrzeni pomiarów
| n | Moc urządzenia (mW) | Moc Urządzenia (dBm) |
|---|---|---|
| 0 | 0.001 | -30 |
| 1 | 0.01 | -20 |
| 2 | 0.1 | -10 |
| 3 | 1 | 0 |
| 4 | 10 | 10 |
| 5 | 100 | 20 |
| 6 | 1000 | 30 |
| 7 | 10000 | 40 |
Jak możemy zobaczyć, moc zmienia się w bardzo szerokim zakresie - od mikrowatów do watów. Przy takim zakresie ciężko jest zauważyć drobne zmiany w dolnej części tabeli, dlatego stosujemy skalę logarytmiczną (czyli dB), która lepiej pokazuje różnice w całym zakresie.
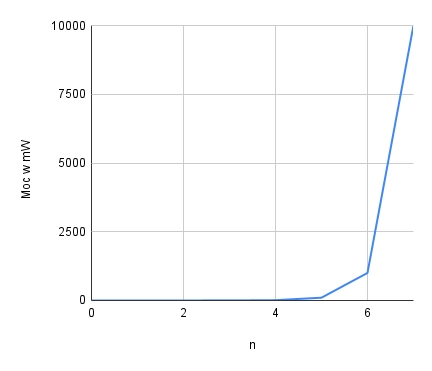
Nasz problem zostaje naprawiony z użyciem decybeli:
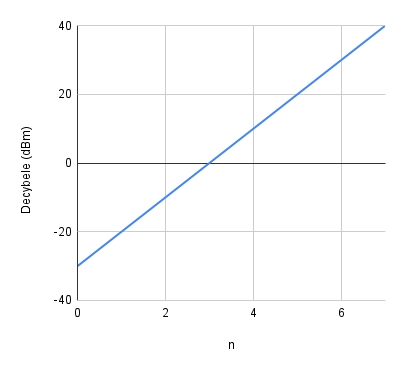
Ale jak to się liczy?
Noi to zależy… Czy porównujemy moc, czy napięcie lub prąd. Jeżeli porównujemy moc to używamy wzoru: $$ dB=10 \log {\frac {P_{1}}{P_0}} $$ A jeżeli napięcie lub prąd: $$ dB = 20\log \frac {U_{1}}{U_0} $$ gdzie symbole z zerem to wartości odniesienia.
Dołóż swoją cegiełkę do tworzenia materiałów edukacyjnych!
Dodawanie i odejmowanie decybeli
Jedną z największych zalet używania decybeli jest to, że możemy po prostu dodawać i odejmować wartości zamiast mnożyć i dzielić. Działa to tak, że jeśli coś wzmacnia sygnał (np. wzmacniacz) to dodajemy dB. Jeśli coś tłumi sygnał (np. kabel) to odejmujemy dB
Przykład
Mamy nadajnik o mocy 30 dBm, antenę o zysku +9 dBi, a kabel tłumi -3 dB: $$ P_{\text{efektywne}}=30 dBm+9 dBi−3 dB=36 dBm $$ Czyli na wyjściu anteny mamy 36 dBm, czyli około 4 waty mocy wypromieniowanej.
dBm, dBi, dBd i inne potworki
Widząc pytania egzaminacyjne pewnie zauważyłeś_aś jednostki dB z czymś na końcu. To coś mówi nam o tym co bierzemy za wartość odniesienia!
- m - moc wyrażona w mW
- i - względem anteny izotropowej
- d - względem dipola
Zadania z egzaminu
- Wzmacniacz posiada wzmocnienie napięciowe 10 razy. Wyraź to wzmocnienie w dB.
To zadanie jest prościutkie bo sprowadza się tylko do podstawienia do wzoru $\frac {U_{1}}{U_0}=10$ $$ dB=20\log 10=20\cdot1=20 \text {dB} $$ 2. Antena kierunkowa daje napięcie 4 razy większe, niż dipol półfalowy zawieszony w tym samym miejscu. Jaki zysk ma antena kierunkowa? $$ dB=20 \cdot \log_{10}(4) \approx 20 \cdot 0.602 = 12.04\ \text{dBd} $$ 3. System antenowy dostarcza sygnał na poziomie -20dBm, jest on podłączony do przedwzmacniacza o wzmocnieniu 10dB kablem o tłumieniu 3dB. Jakiej mocy sygnał uzyskamy na wyjściu przedwzmacniacza? $$ dB=-20dBm+10dB-3dB=-13dBm $$ 4. Napięcie na wejściu odbiornika o oporności 50 om wynosi 10 μV. Napięcie to wzrosło do 100 μV. O ile wzrosło napięcie wyrażone w dB? $$ 20 \cdot \log_{10}\left(\frac{100\ \mu V}{10\ \mu V}\right) = 20 \cdot \log_{10}(10) = 20\ \text{dB} $$